다이얼 룰렛

문제링크

다이얼 룰렛

아이디어

회전 횟수(\(K\))의 범위가 최대 \(10^9\) 인 것에 비해서 수열의 길이(\(N\))은 \(2 \times 10^5\) 밖에 되지 않는다는 점에서 직접 회전시키는 방식은 적용할 수 없습니다. 또한 \(K \gt N\) 라면 반드시 하나 이상의 원소가 중복된다는 것을 알 수 있습니다.

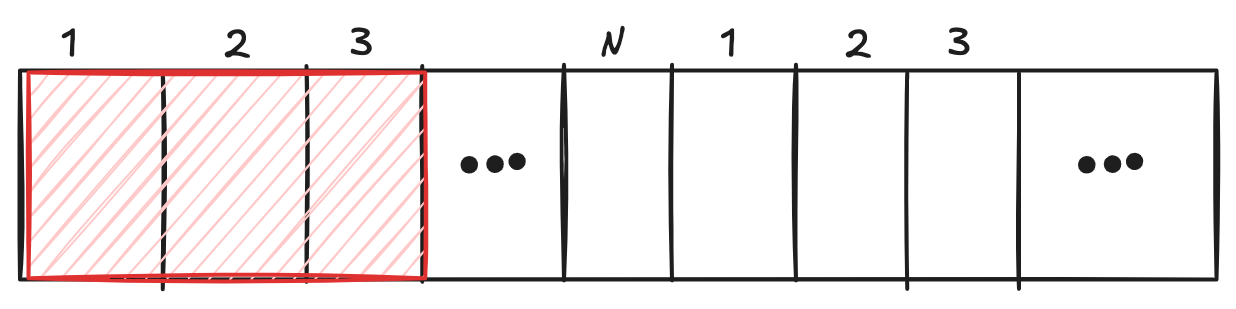
순환 수열을 편하게 설명하기 위하여 아래서부터는 Flat한 수열로 설명하겠습니다.

나올 수 있는 정답의 케이스들을 아래와 같이 3가지로 구분할 수 있습니다.

1. 첫번째 원소를 포함하여 우측 영역까지를 포함하는 경우

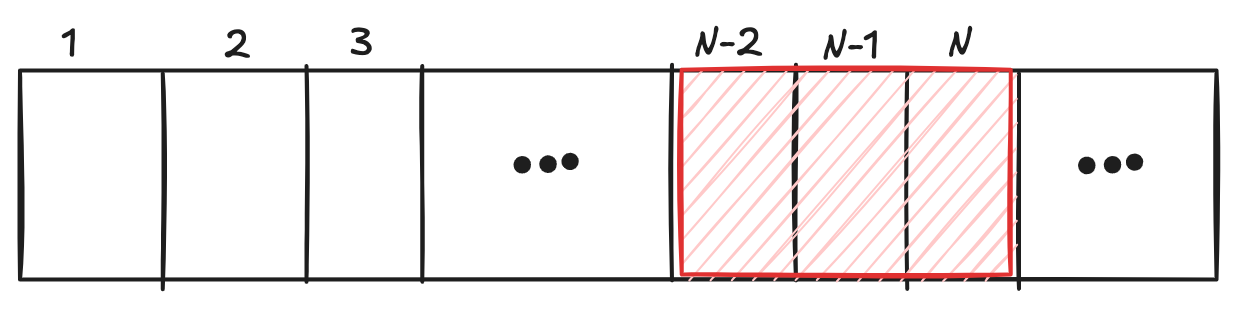
1. 마지막 원소를 포함하여 좌측 영역까지를 포함하는 경우

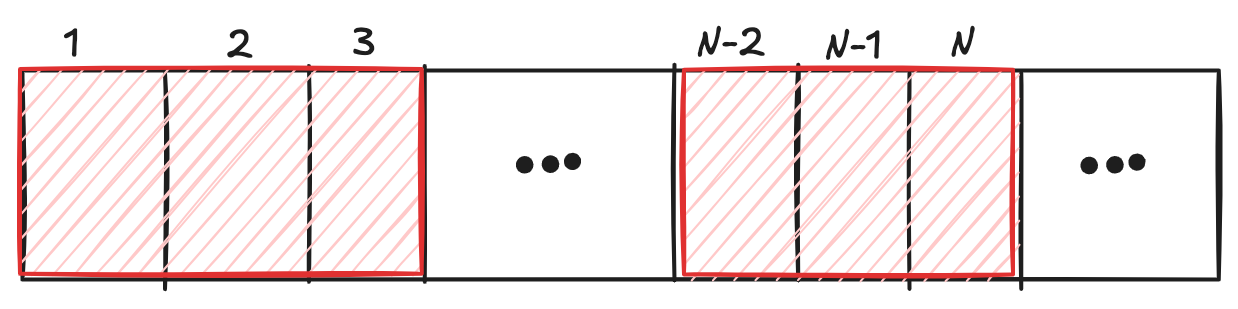
1. 좌측 영역과 우측 영역을 포함하는 경우

3가지 중 3번 케이스에만 적용되는 정답은 나올 수 없습니다. 그 이유를 설명하겠습니다.

• 정답을 수식으로 표현하면 \(\sum \text{선택된 원소} + \text{m} \times \text{선택된 원소의 max값}\) 이 됩니다. (m = K - 회전수)
• 전체의 합을 max로 만들기 위해서, 수열의 범위 내 max값을 최대한 많이 포함시켜야합니다.
  • 회전 수를 줄이고 범위 내 최댓값을 반복하는 것으로 더 나은 최적해를 구성할 수 있습니다.
  • 결국 3번 케이스는 1, 2번 케이스의 답보다 작거나 같은 답을 구성합니다.

위 설명과 마찬가지로 1, 2번 케이스에서도 수열의 범위 내 max값을 최대한 많이 포함시켜야 합니다.

범위 내 max값을 발견한다면 선택되는 원소의 범위를 더 넓히지 않고, 해당 수에서 시계/반시계 회전을 반복하여 max값을 반복적으로 포함시킬 수 있습니다.

즉, 정답은 선택되는 수열의 범위를 먼저 정하고 남은 회전수만큼 끝점의 원소를 더해주면 구할 수 있습니다.

• 1, 2번 케이스에 해당하는 정답은 각각의 누적합 점화식을 사용하여 \(O(1)\) 시간내에 알아낼 수 있습니다.
• 전체 소스코드의 시간 복잡도는 \(O(N)\) 이 됩니다.

소스코드

import java.io.*;
import java.util.*;

public class BOJ_32712 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int[] temp = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
        int N = temp[0], K = temp[1];
        long[] A = Arrays.stream(br.readLine().split(" ")).mapToLong(Long::parseLong).toArray();

        long[] rightSum = new long[N];
        rightSum[0] = A[0];
        for (int i = 1; i < N; i++) {
            rightSum[i] = rightSum[i - 1] + A[i];
        }

        long[] leftSum = new long[N];
        leftSum[0] = A[N - 1];
        for (int i = 1; i < N; i++) {
            leftSum[i] = leftSum[i - 1] + A[N - 1 - i];
        }

        long ans = -1;
        for (int m = 0; m < Math.min(K, N); m++) {
            long result1 = rightSum[m] + Math.max(0, K - m - 1) * A[m];
            long result2 = leftSum[m] + Math.max(0, K - m - 1) * A[N - 1 - m];
            ans = Math.max(ans, Math.max(result1, result2));
        }

        System.out.println(ans);
    }
}