철로

문제링크

철로

아이디어

문제의 요구사항에 따라서 임의의 \(k\) 를 시작점으로 하는 선분은 \([k, k + d]\) 라는 구간으로 표현할 수 있습니다.

처음 문제를 접근하는 순서를 2가지로 표현하면 아래와 같습니다.

1. \(k\)의 범위가 최대 \(2 \times 10^9\)가 될 수 있으므로 가능한 모든 \(k\)에 대해서 탐색을 수행하는 것은 시간초과입니다.
   • 선분이 포함하는 사람들의 수가 변하는 지점은 사람들의 집의 위치 또는 사무실의 위치입니다.
   • \(n\)개의 입력에 대해서 다른 \(n-1\)명의 다른 모든 사람들의 좌표를 확인하는 방법 또한 \(O(N^2)\)로 시간 초과입니다.
2. 다른 모든 사람들의 좌표를 확인하지 않고, 추후에 포함될 수 없는 사람들을 탐색 대상에서 제외하는 방식을 생각해야합니다.

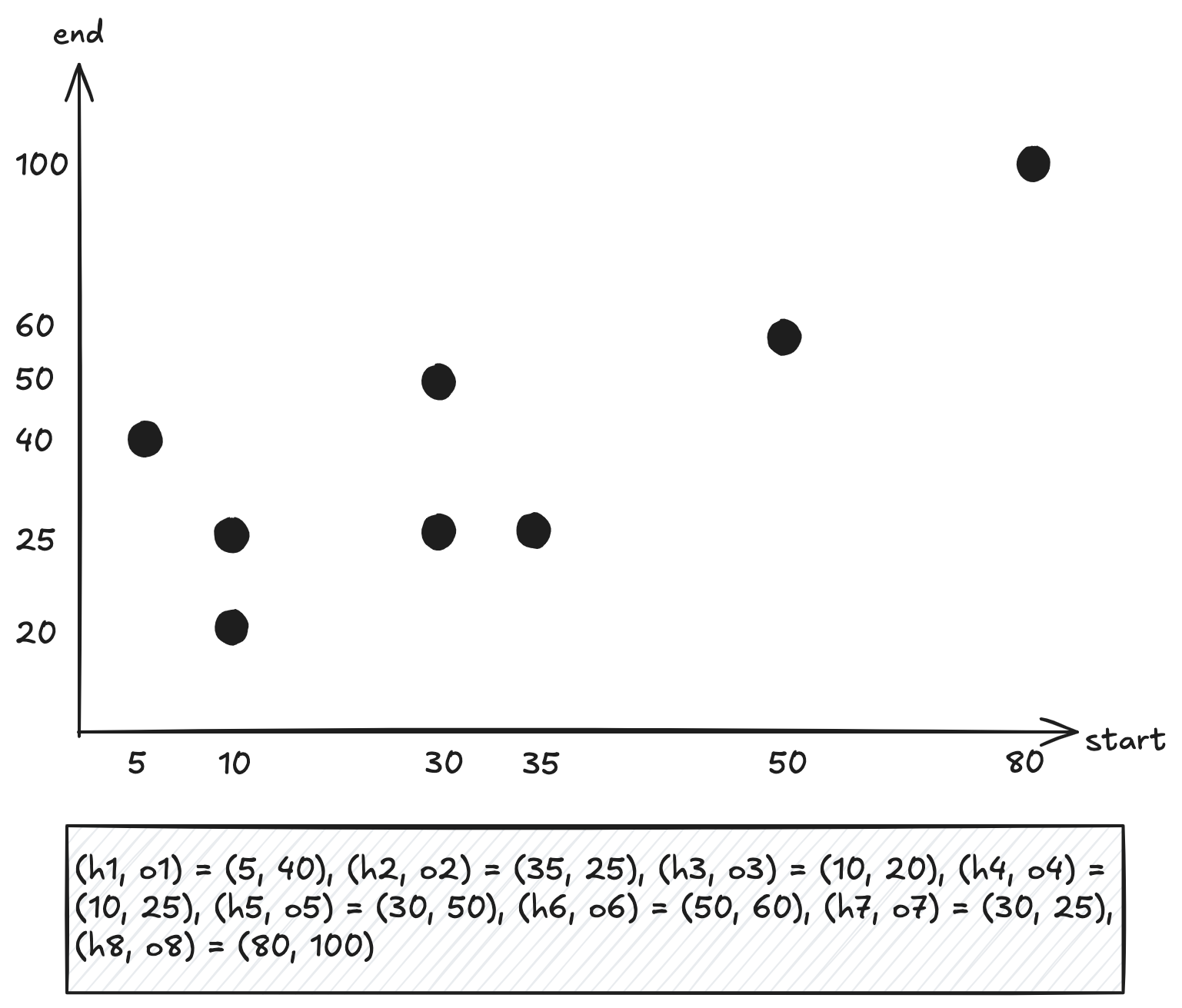
추후에 포함될 수 없는 사람들을 탐색에서 제외하기 위한 방법을 고민하기 위해서 그래프로 도식화해봅시다.

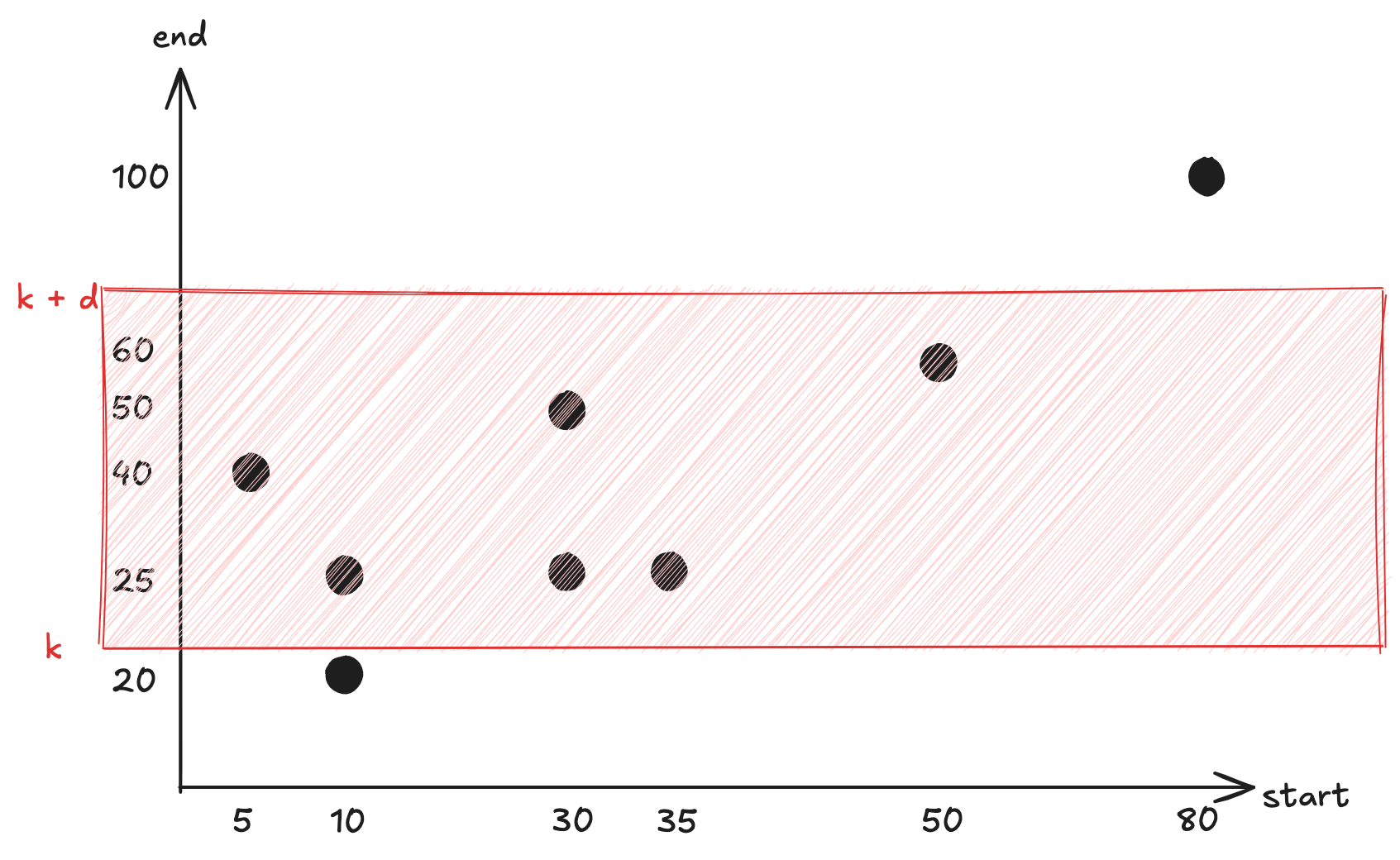
\(k\)에 대해서 구간에 포함되는 영역을 표시하면 아래와 같이 그래프에 표현됩니다.

• 해당 영역에 포함되는 모든 사람들은 철로 선분에 포함됩니다.

사람들의 사무실 위치(end)를 기준으로 \(k\)를 잡게된다면 탐색마다 end가 \(k\)미만의 점들만 제외시키면 됩니다.

과정을 구체화한다면 아래와 같습니다.

1. 최초 Min Heap Tree에는 모든 사람들의 집 위치(start)가 포함된다.
2. \(k\)를 사람들의 사무실 위치(end)를 기준으로 잡고 최솟값부터 탐색을 진행한다.
3. 탐색 과정에서 Heap Tree에서 Min값이 \((k - d)\) 미만인 경우 구간에 포함되지 않고, 추후 탐색에도 포함될 가능성이 없으므로 제거한다.
4. 현재 영역에 포함된 사람들의 수는 3번 과정을 마친 이후 min heap tree에 남아있는 원소의 개수와 같다.
5. 2 - 4번 과정을 \(\text{사람들의 수}(n)\)만큼 반복한다.

소스코드

소스코드

import java.io.*;
import java.util.*;

public class BOJ_13334 {

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        int[][] v = new int[n][];
        PriorityQueue<Integer> pq = new PriorityQueue<>();
        for (int i = 0; i < n; i++) {
            v[i] = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
            if (v[i][0] > v[i][1]) {
                int tmp = v[i][0];
                v[i][0] = v[i][1];
                v[i][1] = tmp;
            }
        }
        int d = Integer.parseInt(br.readLine());
        int ans = 0;
        Arrays.sort(v, (a, b) -> Integer.compare(a[1], b[1]));

        for (int i = 0; i < n; i++) {
            int start = v[i][1] - d;
            pq.add(v[i][0]);
            while (!pq.isEmpty() && pq.peek() < start) {
                pq.poll();
            }
            ans = Math.max(ans, pq.size());
        }
        System.out.println(ans);
    }

}